Attività settimanale

  • Introduzione

    • Seminari per l'esame

    • Riferimenti: 


    • Modalità d'esame

      L'esame consiste in un seminario su un argomento inerente al corso.

      Gli studenti possono proporre un argomento di loro interesse; in alternativa, possono scegliere un argomento tra quelli sotto elencati:

      • Il lemma di Hensel (rif. Gouvea ch 3 e 6)

      • Serie e polinomi p-adici (rif. Gouvea ch 3 e 6)

      • La dimostrazione idelica del teorema di finitezza del gruppo delle classi e del teorema delle unità (rif. Cassels Frohlich Ch. II)

      • Teoria di Lubin Tate (rif. Milne Ch. I)

      • Gruppo di Brauer (rif. Milne Ch. IV)

      • Il teorema di Tate e Nakayama (Rif. Serre)

      • Esponenziale e logaritmo p-adici (Robert pp 251-263)

      • Coomologia degli idèles e dimostrazione dei teoremi della teoria del corpo di classe globale (rif. Milne Cap. VII)

      • Classificazione delle forme quadratiche su un campo di numeri (rif. Milne Cap. VIII)




  • Lezione 1 - 16 Gennaio 2024

    Introduzione al corso Teoria di Galois e gruppi profiniti.

  • Lezione 2 - 17 Gennaio 2024

    Valutazioni p-adiche sui razionali. Campi valutati e completamenti.

  • Lezione 3 - 22 Gennaio 2024

    Campi locali. Estensioni di valori assoluti in campi locali. Teoria della ramificazione nei campi locali: indice di ramificazione e grado residuo. Estensioni non ramificate e totalmente ramificate. Esistenza della sottoestensione massimale non ramificata di una estensione data. Teoria di Galois dei campi locali. Gruppo di interzia. Gruppi di ramificazione.

  • Lezione 4 - 30 Gennaio 2024

    Aritmetica dei campi globali. Domini di Dedekind, ideali frazionari e gruppo delle classi. Finitezza del gruppo delle classi di ideali per un campo di numeri. Teorema delle unità di Dirichlet. Decomposizione degli ideali primi. Valutazioni su un campo globale. Teorema di Ostrowski. Formula del prodotto.

  • Lezione 5 - 1 Febbraio 2024

    Discriminante e ramificazione. L'anello degli adèles, il gruppo degli idèles e la loro topologia. Norma idelica. Idèles e ideali. Gruppo delle classi degli idèles. Dimostrazione idelica della finitezza del gruppo delle classi e del teorema delle unità di Dirichlet.

    . 

  • Lezione 6 - 13 Febbraio 2024

    Struttura delle estensioni locali non ramificate. Elemento di Frobenius. Proprietà delle estensioni abeliane. Decomposizione dei primi nei campi ciclotomici. La legge di reciprocità quadratica. Definizione della mappa di Artin di un'estensione abeliana di Q supponendo vero il teorema di Kronecker Weber.

  • Lezione 7 - 14 Febbraio 2024

    Esistenza della mappa di reciprocità locale e sue proprietà. Applicazione: il teorema di Kronecker- Weber locale.

  • Lezione 8 - 20 Febbraio 2024

    Conduttore di un'estensione abeliana. Deduzione del teorema di Kronecker Weber globale da quello locale. Coomologia di gruppi: G-moduli, moduli iniettivi, risoluzioni iniettive. Coomologia di un G-modulo. Una successione esatta corta di G-moduli induce una successione esatta lunga in coomologia. Dimesnsion shifting. Risoluzioni acicliche. Moduli indotti e lemma di Shapiro.

  • Lezione 9 - 22 Febbraio 2024

    Moduli indotti. Calcolo esplicito della coomologia di un G-modulo. Cocatene, cocicli, cobordi omogenei e non omogenei. Interpretazione di 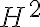H^2 come insieme delle classi di isomorfismo di estensioni. Funtorialità della comologia rispetto ai gruppi: omomorfismi di restrizione, corestrizione, inflazione. Omologia di gruppi. Isomorfismo canonico H_1(G,\mathbb{Z})\simeq G^{ab}.

  • Lezione 10 - 19 Marzo 2024

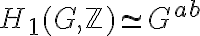    Gruppi di coomologia di Tate. Coomologia di Tate dei gruppi ciclici finiti e quoziente di Herbrand. Coomologia dei gruppi profiniti. Teoremi fondamentali di coomologia galoisiana: teorema 90 di Hilbert, suriettività della norma sulle unità nel caso di estensioni non ramificate. Gruppo di Brauer.

  • Lezione 11 - 25 Marzo 2024

    Dimostrazione dei seguenti due risultati, dato un campo locale K:
    • L'inflazione
      H^2(K^{nr}/K)\rightarrow H^2(\overline{K}/K)
      è un isomorfismo;
    • Esiste un isomorfismo
        inv_K:H^2(\overline{K}/K)\rightarrow \mathbb{Q}/\mathbb{Z}

  • Lezione 12 - 26 Marzo 2024

    Esistenza della mappa  di reciprocità locale, teorema di limitazione delle norme e teorema di esistenza.

  • Lezione 13 - 9 Aprile 2024

    Legge di reciprocità globale e teorema di esistenza in forma adelica. Schema della dimostrazione. La successione esatta fondamentale per il gruppo di Brauer.


  • Lezione 14 - 11 Aprile 2024

    La legge di reciprocità globale in termini di ideali frazionari. Omomorfismi ammissibili sul gruppo degli ideali frazionari e fattorizzabilità tramite il gruppo delle classi di idèles. Moduli e ray class groups associati. Esempi. Narrow class group. Sottogruppi di congruenza degli ideali frazionari.

  • Lezione 15 - 15 Aprile 2024

    Ray class field associato a un modulo. Conduttore di un'estensione abeliana. Corpo di Hilbert e teorema dell'ideale principale. Esempi. Teorema di densità di Chebotarev.
    Cenni su possibili approcci al caso non abeliano, rappresentazioni galoisiane e forme automorfe. Corrispondenza di Langlands globale e locale e funzioni L.